# 链表

# No.1 反转链表

反转一个单链表。

输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

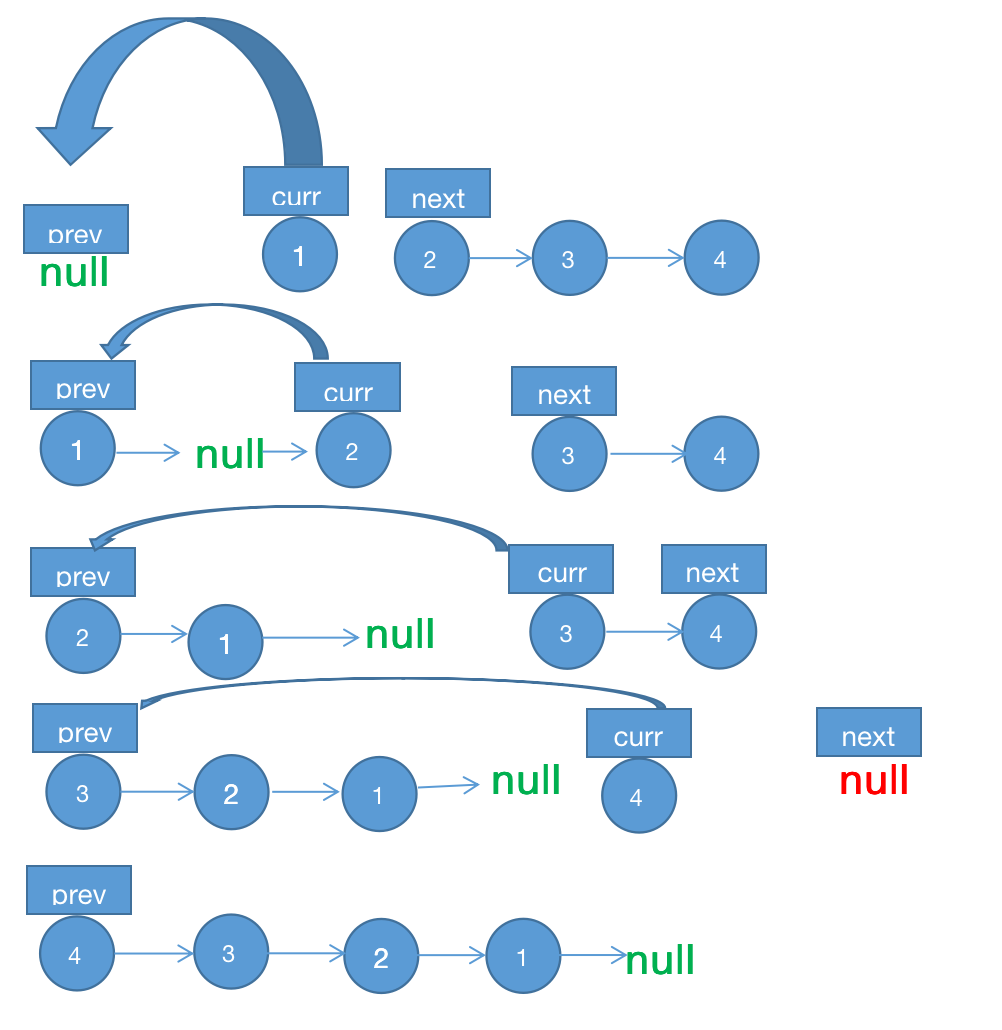
解法一：迭代

时间复杂度: O(n)
空间复杂度: O(1)

function Node(key) {
    this.key = key;
    this.next = null;
}
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
const reverseList = (head) => {
    if (!head) {
        return null
    }
    let prev = null, curr = head;
    while (curr) {
        let next = curr.next
        curr.next = prev
        prev = curr
        curr = next
        // [curr.next, prev, curr] = [prev, curr, curr.next]
    }
    return prev
}

设置哨兵节点 null, 初始化当前节点 curr 为 head
将当前节点 curr 的指针指向上一个节点 prev
更新上一个节点 prev 为当前节点 curr
更新当前节点 curr 为下一个节点 next
重复以上动作直到当前节点为尾节点的节点 null

解法二: 尾递归

其实就是解法一的简化版

时间复杂度: O(n)
空间复杂度: O(1)

const reverseList = (head) => {
    let reverse = (prev, curr) => {
        if (!curr) return prev
        let next = curr.next
        curr.next = prev
        return reverse(curr, next)
    }
    return reverse(null, head)
}

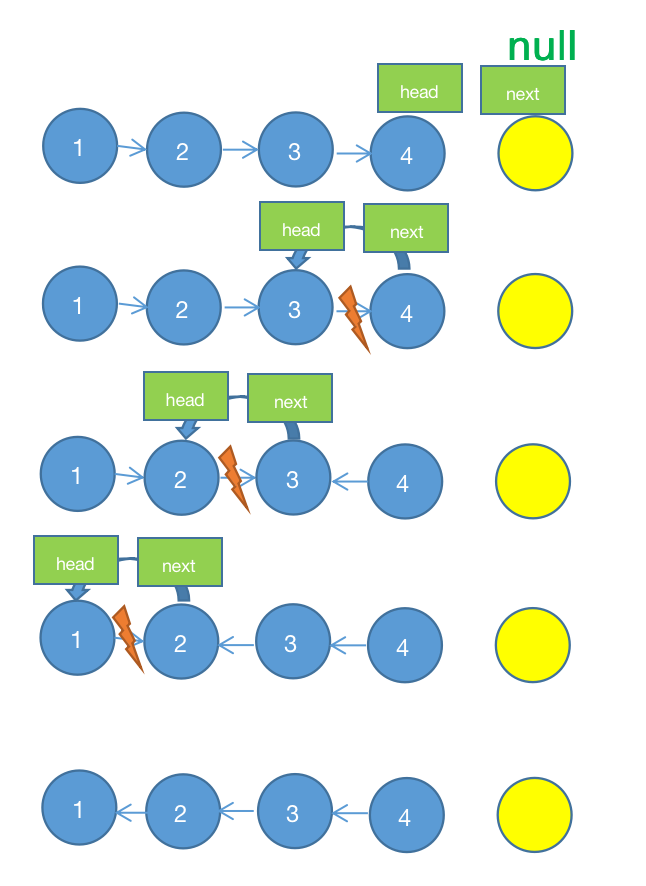
解法三: 递归

不断递归反转当前节点 head 的后继节点 next

时间复杂度: O(n)
空间复杂度: O(n)

const reverseList = (head) => {
    if (!head || !head.next) return head
    let next = head.next
    // 递归反转
    let reverse = reverseList(next)
    // 变更指针
    head.next = null
    next.next = head
    return reverse
}

当前节点 head，下一个节点 next
将 head 的指针断开，把 head.next 指向 head，即是反转
由编译器函数调用执行栈原理可知，最先调用的函数会在递归过程中最后被执行，而最后调用的会最先执行
因此此题，最先返回最后两个节点开始反转操作，依次从后面两两节点开始反转

# No.2 区间反转

反转从位置 m 到 n 的链表。请使用一趟扫描完成反转。

输入: 1->2->3->4->5->NULL, m = 2, n = 4
输出: 1->4->3->2->5->NULL

解法一: 迭代

核心解法: 即将需要反转的 m 到 n 区间的链表反转，再重新连接首尾即可

const reverseList4 = (head, m, n) => {
    // 保存原节点
    let dummy = new Node()
    dummy.next = head

    // 默认节点
    let tmpHead = dummy

    // 找到第m-1个节点
    for (let i = 0; i < m - 1; i++) {
        tmpHead = tmpHead.next
    }

    // 区间反转
    let prev = null, curr = tmpHead.next
    for (let i = 0; i <= n - m; i++) {
        let next = curr.next
        curr.next = prev
        prev = curr
        curr = next
    }

    // 将翻转的部分链表和原链表 拼接
    tmpHead.next.next = curr
    tmpHead.next = prev

    return dummy.next
}

也可以写成

const reverseList4 = (head, m, n) => {
    // 保存原节点
    let dummy = new Node()
    dummy.next = head

    // 默认节点
    let tmpHead = dummy
    let pos = 0

    // 找到第m-1个节点
    while (pos < m-1) {
        tmpHead = tmpHead.next
        pos++
    }

    // 区间反转
    let prev = null, curr = tmpHead.next
    while (pos < n) {
        let next = curr.next
        curr.next = prev
        prev = curr
        curr = next
        pos++
    }

    // 将翻转的部分链表和原链表 拼接
    tmpHead.next.next = curr
    tmpHead.next = prev

    return dummy.next
}

解法二: 迭代2

const reverseList5 = (head, m, n) => {
    if (!head) return null

    // 第m-1个节点 & 第m个节点
    let prev = null, curr = head
    while (m > 1) {
        prev = curr
        curr = curr.next
        m--
        n--
    }
    // 区间反转
    let con = prev, tail = curr
    while (n > 0) {
        let next = curr.next
        curr.next = prev
        prev = curr
        curr = next
        n--
    }
    // 解决环
    if (con != null) {
        con.next = prev
    } else {
        head = prev
    }
    tail.next = curr

    return head
}

解法三: 递归

# No.3 两个一组反转

给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。

你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

给定 1->2->3->4, 你应该返回 2->1->4->3.

二分搜索 undefined与null的区别

No.1 反转链表

No.2 区间反转

No.3 两个一组反转