# 堆
我们将要学习一种特殊的二叉树,也就是堆数据结构,也叫作二叉堆。
二叉堆是计算机科学中一种非常著名的数据结构,由于它能高效、快速地找出最大值和最小值,常被应用于优先队列。
# 定义
- 它是一棵完全二叉树,表示树的每一层都有左侧和右侧子节点(除了最后一层的叶节点),并且最后一层的叶节点尽可能都是左侧子节点,这叫作结构特性。
- 二叉堆不是最小堆就是最大堆。最小堆允许你快速导出树的最小值,最大堆允许你快速导出树的最大值。所有的节点都大于等于(最大堆)或小于等于(最小堆)每个它的子节点。这叫作堆特性。
下图展示了一些合法的和不合法的堆。
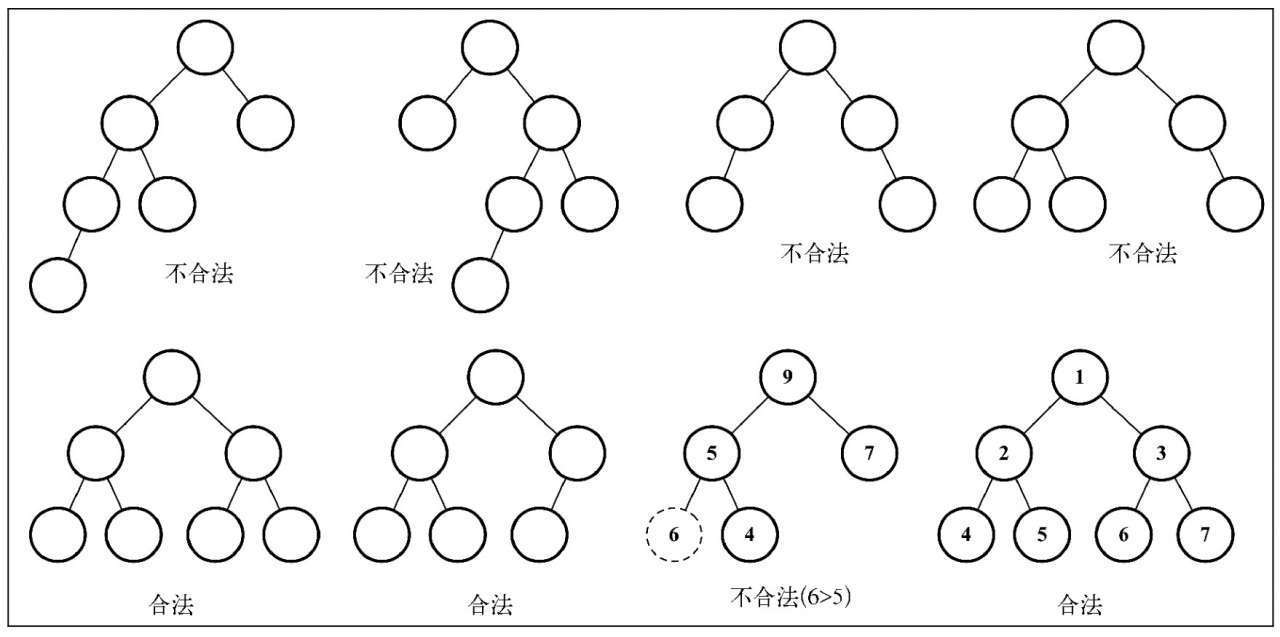
- 每个子节点都要大于等于父节点(小于等于父节点)
- 当父节点大于或等于(小于或等于)它的每一个子节点时,称为最大堆(最小堆)
class Heap {
constructor() {
// 父节点 和 传进的值 对比
this.compareFn = (a, b) => {
return a >= b
}
// 交换节点位置
this.swap = (array, a, b) => {
[array[a], array[b]] = [array[b], array[a]]
}
this.heap = []
}
// 获取左侧子节点
getLeftIndex(index) {
return 2 * index + 1
}
// 获取右侧子节点
getRightIndex(index) {
return 2 * index + 2
}
// 获取父节点
getParentIndex(index) {
if (index === 0) {
return undefined
}
return Math.floor((index - 1) / 2)
}
// 最小值
findMinimum() {
return this.isEmpty() ? undefined : this.heap[0]
}
size() {
return this.heap.length
}
isEmpty() {
return this.size() === 0
}
}
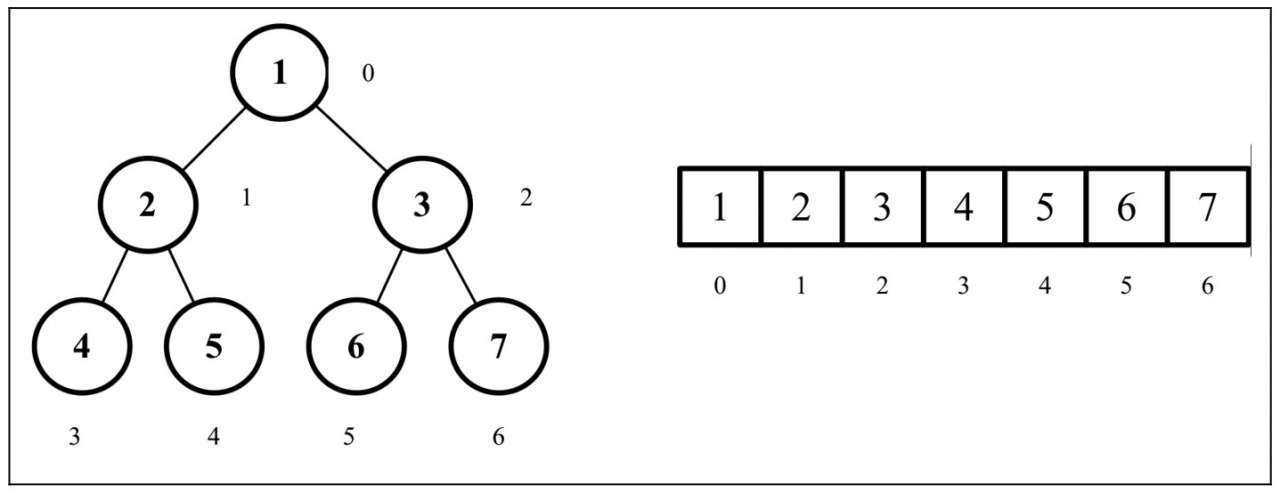
# 最小堆
向堆中插入值是指将值插入堆的底部叶节点(数组的最后一个位置), 然后再执行siftUp方法,表示我们将要将这个值和它的父节点进行交换,直到父节点小于这个插入的值
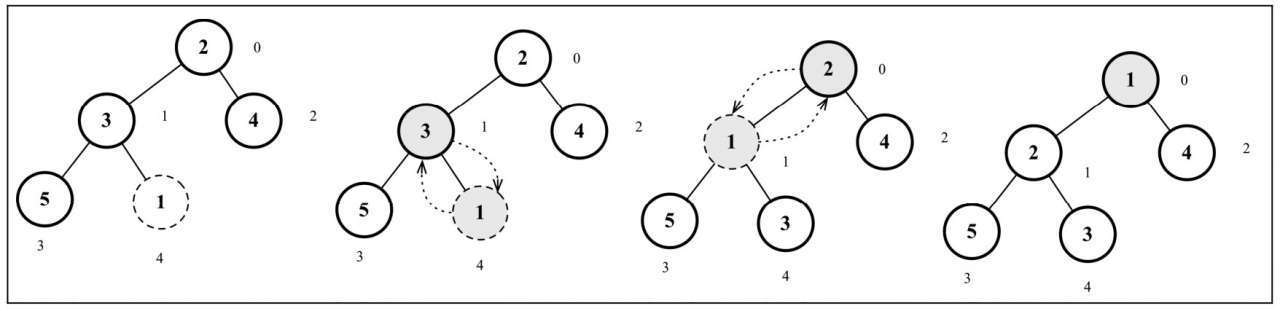
// 向堆中插入值
insert(value) {
if (value != null) {
this.heap.push(value)
this.siftUp(this.heap.length - 1) // 当前索引
return true
}
return false
}
// 上浮
siftUp(index) {
// 将要将这个值和它的父节点进行交换,直到父节点小于这个插入的值
let parent = this.getParentIndex(index)
while ( index > 0 && this.compareFn(this.heap[parent], this.heap[index])) {
this.swap(this.heap, parent, index)
index = parent
parent = this.getParentIndex(index)
}
}
const heap = new Heap()
heap.insert(2)
heap.insert(3)
heap.insert(4)
heap.insert(5)
heap.insert(1)
console.log(heap.heap) // [1, 2, 4, 5, 3]
导出堆中的最小值或最大值
移除最小值(最小堆)或最大值(最大堆)表示移除数组中的第一个元素(堆的根节点)。在移除后,我们将堆的最后一个元素移动至根部并执行siftDown函数,表示我们将交换元素直到堆的结构正常。
siftDown(index) {
const left = this.getLeftIndex(index)
const right = this.getRightIndex(index)
if (
this.compareFn(this.heap[index], this.heap[left]) &&
this.compareFn(this.heap[index], this.heap[right])
) {
if (!this.compareFn(this.heap[right], this.heap[left])) {
this.swap(this.heap, right, index)
this.siftDown(right)
} else {
this.swap(this.heap, left, index)
this.siftDown(left)
}
} else if (this.compareFn(this.heap[index], this.heap[left])) {
this.swap(this.heap, left, index)
this.siftDown(left)
} else if (this.compareFn(this.heap[index], this.heap[right])) {
this.swap(this.heap, right, index)
this.siftDown(right)
}
}
// 导出堆中的最小值或最大值
extract() {
if (this.isEmpty()) {
return undefined
}
if (this.size() === 1) {
return this.heap.shift()
}
const removedValue = this.heap[0]
this.heap[0] = this.heap.pop()
this.siftDown(0)
return removedValue
}
for (let i = 1; i < 10; i++) {
heap.insert(i)
}
console.log(heap.extract()) // 1
console.log(heap.heap) // [2, 4, 3, 8, 5, 6, 7, 9]
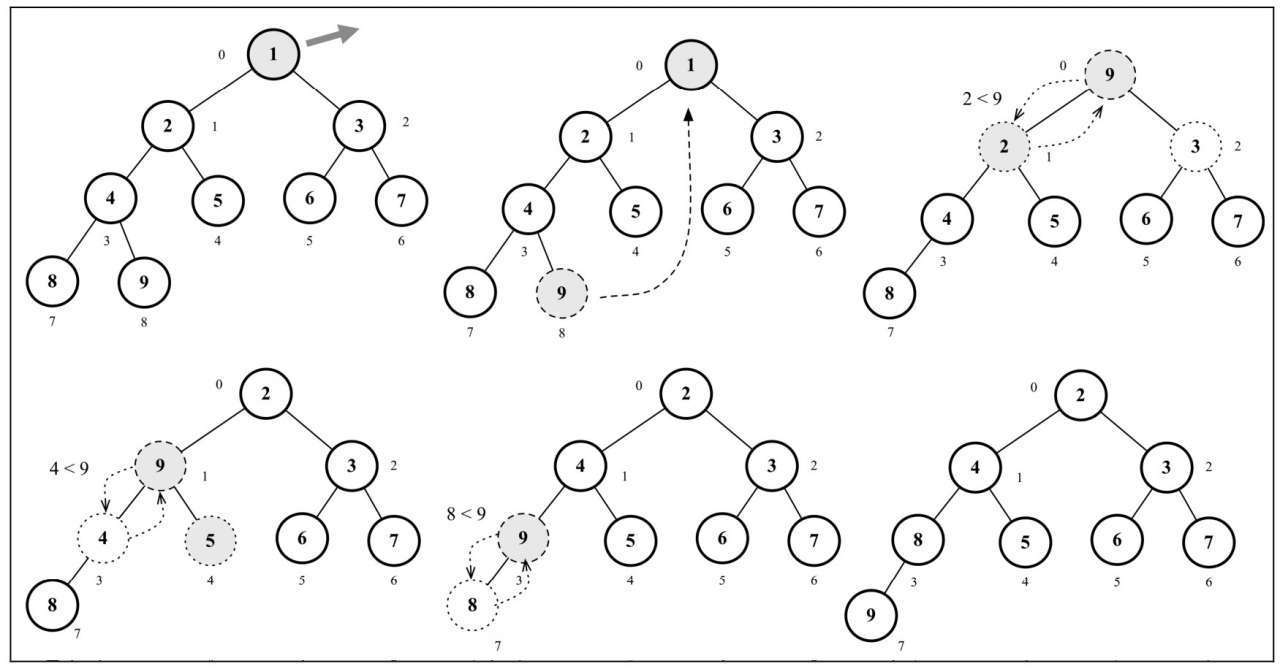
# 最大堆
修改这个方法即可
this.compareFn = (a, b) => {
return a < b
}
# 堆排序
??